我们现在将支持向量机推广到回归问题，同时保持它的稀疏性。在简单的线性回归模型中，我们最小化一个正则化的误差函数

$$\frac{1}{2}\sum\limits_{n=1}^N\{y_n - t_n\}^2 + \frac{\lambda}{2}\Vert w \Vert^2 \tag{7.50}$$

为了得到稀疏解，二次误差函数被替换为一个$\epsilon$-不敏感误差函数（$\epsilon$-insensitive error function）（Vapnik, 1995）。如果预测$y(x)$和目标$t$之间的差的绝对值小于$\epsilon$，那么这个误差函数给出的误差等于零，其中$\epsilon > 0$。$epsilon$-不敏感误差函数的一个简单的例子是

$$E_\epsilon(y(x) - t) = \begin{cases} 0, if \vert y(x) - t \vert < \epsilon; \\ \vert y(x) - t \vert - \epsilon, otherwise \end{cases} \tag{7.51}$$

它在不敏感区域之外，会有一个与误差相关联的线性代价。如图7.6所示。

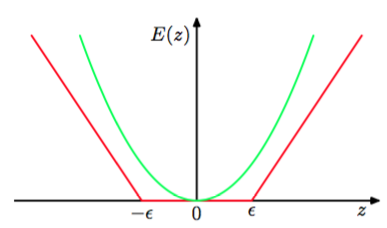
图 7.6 $\epsilon$-不敏感误差函数（红色）在不敏感区域之外,误差函数值随着距离线性增大。作为对比，同时给出了二次误差函数（绿色）。

于是我们最小化正则化的误差函数，形式为

$$C\sum\limits_{n=1}^NE_{\epsilon}(y(x) - t_n) + \frac{1}{2}\Vert w \Vert^2 \tag{7.52}$$

其中$y(x)$由式（7.1）给出。按照惯例，（起着相反作用的）正则化参数被记作$C$，出现在误差项之前。

与之前一样，通过引入松弛变量的方式，我们可以重新表达最优化问题。对于每个数据点$x$，我们现在需要两个松弛变量$\xi \geq 0$和$\xi \geq 0$，其中$\xi > 0$对应于$t > y(x) + \epsilon$的数据点，$\hat{\xi} > 0$对应于$t_n < y(x_n) − \epsilon$的数据点，如图7.7所示。

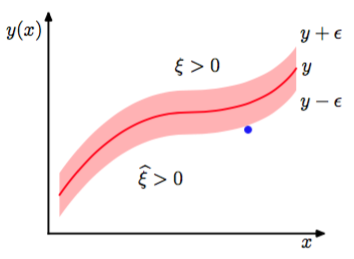
图 7.7 SVM回归的说明。图中画出了回归曲线以及$\epsilon$-不敏感“管道”。同时给出的是松弛变量$\xi$和$\hat{\xi}$的例子。对于$\epsilon$-管道上方的点，$\xi > 0$且$\xi = 0$，对于$\epsilon$-管道下方的点，$\xi = 0$且$\xi > 0$，对于$\epsilon$-管道内部的点$\xi = \hat{\xi} = 0$。

目标点位于$\epsilon$-管道内的条件是$y_n − \epsilon \leq t_n \leq y_n + \epsilon$，其中$y_n = y(x_n)$。引入松弛变量使得数据点能够位于管道之外，只要松弛变量不为零即可。对应的条件变为

$$\begin{eqnarray} t_n \leq y(x_n) + \epsilon + \xi_n \tag{7.53} \\ t_n \geq y(x_n) - \epsilon - \hat{\xi_n} \tag{7.54} \end{eqnarray}$$

这样，支持向量回归的误差函数就可以写成

$$C\sum\limits_{n=1}^N(\xi_n + \hat{\xi_n} + \frac{1}{2}\Vert w \Vert^2) \tag{7.55}$$

它必须在限制条件$\xi_n \geq 0$和$\hat{\xi_n} \geq 0$和式（7.53），（7.54）下进行最小化。通过引入拉格朗日乘数$a_n \geq 0, a_n \geq 0, \mu_n \geq 0$以及$\mu_n \geq 0$，然后最优化拉格朗日函数

$$\begin{eqnarray} L = &C& \sum\limits_{n=1}^N(\xi_n + \hat{\xi_n}) + \frac{1}{2}\Vert w \Vert^2 - \sum\limits_{n=1}^N(\mu_n\xi_n + \hat{\mu_n}\hat{\xi_n}) \\ &-& \sum\limits_{n=1}^Na_n(\epsilon + \xi_n + y_n - t_n) - \sum\limits_{n=1}^N\hat{a_n}(\epsilon + \hat{\xi_n} - y_n + t_n) \tag{7.56} \end{eqnarray}$$

我们现在使用式（7.1）替换$y(x)$，然后令拉格朗日函数关于$w, b, \xi_n$和$\xi_n$的导数为0，得到：

$$\begin{eqnarray} \frac{\partial L}{\partial w} = 0 &\rightarrow& w = \sum\limits_{n=1}^N(a_n - \hat{a}_n)\phi(x_n) \tag{7.57} \\ \frac{\partial L}{\partial b} = 0 &\rightarrow& \sum\limits_{n=1}^N(a_n - \hat{a}_n) = 0 \tag{7.58} \\ \frac{\partial L}{\partial \xi_n} = 0 &\rightarrow& a_n + \mu_n = C \tag{7.59} \\ \frac{\partial L}{\partial \hat{\xi_n}} = 0 &\rightarrow& \hat{a}_n + \hat{\mu}_n = C \tag{7.60} \end{eqnarray}$$

使用这些结果消去拉格朗日函数中对应的变量，我们看到对偶问题涉及到关于$\{a_n\}$和$\{\hat{a}_n\}$最大化

$$\begin{eqnarray} \tilde{L}(a,\hat{a}) = &-&\frac{1}{2}\sum\limits_{n=1}^N\sum\limits_{m=1}^N(a_n - \hat{a}_n)(a_m - \hat{a}_m)k(x_n,x_m) \\ &-&\epsilon\sum\limits_{m=1}^N(a_n - \hat{a}_n) + \sum\limits_{m=1}^N(a_n - \hat{a}_n)t_n \tag{7.61} \end{eqnarray}$$

其中我们已经引入了核$k(x, x') = \phi(x)^T\phi(x')$。与之前一样，这是一个具有限制条件的最大化问题。为了找到限制条件，我们注意到，因为$a_n, \hat{a}_n$是拉格朗日乘数，所以它们要满足$a_n \geq 0$和$\hat{a}_n \geq 0$必须成立。且$\mu_n \geq 0$和$\hat{\mu}_n \geq 0$以及式（7.59）（7.60）要求$a_n \leq C$且$\hat{a}_n \leq C$，因此我们又一次得到盒限制

$$\begin{eqnarray} 0 \leq a_n \leq C \tag{7.62} \\ 0 \leq \hat{a}_n \leq C \tag{7.63} \end{eqnarray}$$

以及条件（7.58）。

将式（7.57）代入式（7.1），我们看到对于新的输入变量，可以使用

$$y(x) = \sum\limits_{n=1}^N(a_n - \hat{a}_n)k(x,x_n) + b \tag{7.64}$$

进行预测，这又一次被表示为核函数的形式。

对应的Karush-Kuhn-Tucker（KKT）条件说明了在解的位置，对偶变量与限制的乘积必须等于0，形式为

$$\begin{eqnarray} a_n(\epsilon + \xi_n + y_n - t_n) &=& 0 \tag{7.65} \\ \hat{a}_n(\epsilon + \hat{\xi}_n + y_n - t_n) &=& 0 \tag{7.66} \\ (C - a_n)\xi_n &=& 0 \tag{7.67} \\ (C - \hat{a}_n)\hat{\xi}_n &=& 0 \tag{7.68} \end{eqnarray}$$

根据这些条件，我们能得到一些有用的结果。首先，我们注意到如果$\epsilon + \xi_n + y_n − t_n = 0$，那么系数$a_n$只能非零，这表明数据点要么位于$\epsilon$-管道的上边界上（$\xi_n = 0$），要么位于上边界的上方（$\xi > 0$）。类似地，$\hat{a}_n$的非零值表示$\epsilon + \xi − y_n + t_n = 0$，这些点必须位于$\epsilon$-管道的下边界上或下边界的下方。

此外，由于将两式相加，注意到$\xi_n$和$\hat{\xi}_n$是非负的，而$\epsilon$是严格为正的，因此对于每个数据点$x_n,a_n$或$\hat {a}_n$至少一个为0，或都为0。所以$\epsilon + \xi_n + y_n − t_n = 0$和$\epsilon + \xi_n − y_n + t_n = 0$这两个限制是不兼容的。

支持向量是对于由式（7.64）给出的预测有贡献的数据点，换句话说，就是那些使得$a_n \neq 0$或$\hat{a}_n \neq 0$成立的数据点。这些数据点位于$\epsilon$-管道边界上或者管道外部。管道内部的所有点都有$a_n = \hat{a}_n = 0$。我们又一次得到一个稀疏解，在预测模型（7.64）中唯一必须计算的项就是涉及到支持向量的项。

参数$b$可以通过，考虑一个数据点，满足$0 < a_n < C$。根据式（7.67），一定有$\xi_n = 0$，根据式（7.65），一定有$\epsilon + y_n − t_n = 0$。使用式（7.1），然后求解$b$得到。这时我们有

$$\begin{eqnarray} b &=& t_n - \epsilon - w^T\phi(x_n) \\ &=& t_n \epsilon - \sum\limits_{m=1}^N(a_m - \hat{a}_m)k(x_n,x_m) \tag{7.69} \end{eqnarray}$$

其中我们使用了式（7.57）。通过考虑一个满足$0 < a_n < C$的数据点，我们可以得到一个类似的结果。在实际应用中，更好的做法是对所有的这些b的估计进行平均。

与分类问题的情形相同，有另一种用于回归的SVM的形式。这种形式的SVM中，控制复杂度的参数有一个更加直观的意义(Scholkopf et al., 2000)。特别地，我们不固定不敏感区域$\epsilon$的宽度，而是固定位于管道外部的数据点的比例$v$。这涉及到最大化

$$\begin{eqnarray} \tilde{L}(a,\hat{a}) = &-&\sum\limits_{n=1}^N\sum\limits_{m=1}^N(a_n - \hat{a}_n)(a_m - \hat{a}_m)k(x_n,x_m) \\ &+&\sum\limits_{m=1}^N(a_n - \hat{a}_n)t_n \tag{7.70} \end{eqnarray}$$

限制条件为

$$\begin{eqnarray} 0 \leq a_n &\leq& \frac{C}{N} \tag{7.71} \\ 0 \leq \hat{a}_n &\leq& \frac{C}{N} \tag{7.72} \\ \sum\limits_{n=1}^N(a_n - \hat{a}_n) &=& 0 \tag{7.73} \\ \sum\limits_{n=1}^N(a_n + \hat{a}_n) &\leq& vC \tag{7.74} \end{eqnarray}$$

可以证明至多有$vN$个数据点落在不敏感管道外部，而至少有$vN$个数据点是支持向量，因此位于管道上或者管道外部。

图7.8说明了使用支持向量机解决回归问题的一个例子，数据集使用的是正弦曲线数据集。

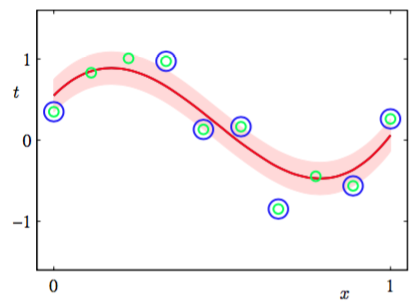
图 7.8 $v$-SVM回归应用到人工生成的正弦数据集上的说明，SVM使用了高斯核。预测分布曲线为红色曲线，$\epsilon$-不敏感管道对应于阴影区域。此外，数据点用绿色表示，支持向量用蓝色圆圈标记。

这里参数$v$和$C$已经手动选择完毕。在实际应用中，它们的值通常通过交叉验证的方法确定。