现在把线性判别式推广到个类别的情况,我们可能会尝试组合多个二分类判别式来构造一个类判别式。然而这会导致一些现在要展示的严重问题(Duda and Hart, 1973)。
考虑一个包含个把属于类别的点与其它的区分开的分类器。这被称为一对其他(one-versus-the-rest)分类器。图4.2的左手边展示了一个涉及三个类别的例子,这种方法会导致空间中有一块类别含糊不清的区域。
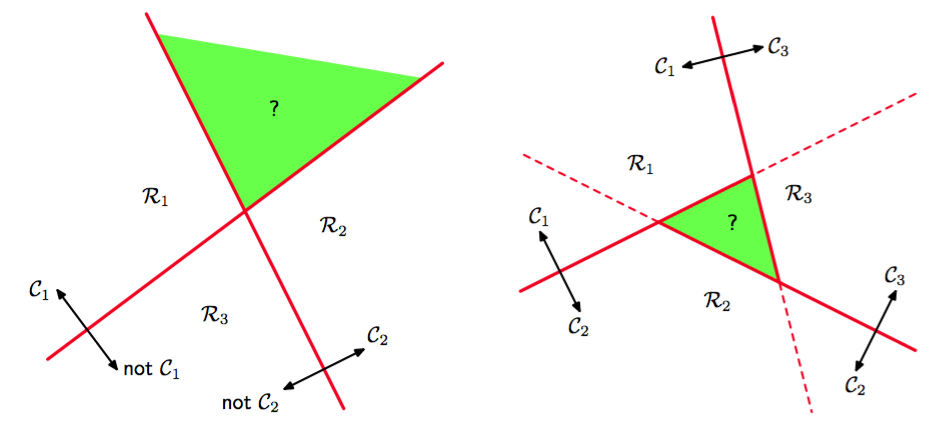
图 4.2 一对其他分类方法
另一种方法是引入个二元判别函数,对每一对类别都设置一个。这被称为一对一(one-versus-one)分类器。然后根据这些判别函数的大多数投票来确定每个点的类别。然而这也会引起类别含糊不清的区域的问题,图4.2的右手边展示。
引入包含个形式为
的线性函数的单个类判别式,并把点分入对于所有都有的类中,就可以避免这些问题。类间的决策边界由给出,它对应形式为
的维的超平面。这与4.1.1节讨论的二分类情况下的决策边界具有相同的形式,因此也有类似的几何性质。
这样的判别式得到的决策区域总是单连通且凸的。为了证明这个,让我们考虑图4.3中展示的,两个都位于决策区域中的点。
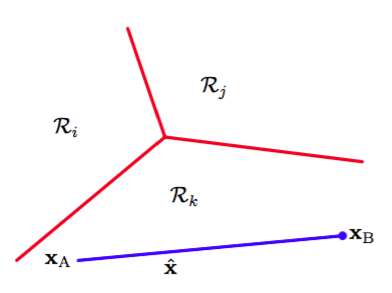
图 4.3 多类判别函数的决策区域的说明
任何一个在连接线段上的点可以表示为
其中。根据判别函数的线性性,可以得到
因为都在中,所以对于所有都满足,所以,所以在中。因此是单连通且凸的。
注意,对于二分类的情形,我们既可以使用这里讨论的基于两个判别函数方法,也可以使用4.1.1节给出基于单一的判别函数的更简单的但等价的方法。
现在,我们开始探讨三种线性判别函数的参数学习方法,即基于最小二乘、Fisher线性判别式,以及感知器算法。